Supervised Speech Enhancement with Self-Attention

About This Article

Before diving right in, it would be a great idea to check out this awesome piece on Transformers and The Attention Mechanism written by one of the most insightful AI bloggers, Lilian Weng. Since these concepts form the backbone of the architecture used in the model we're using, getting familiar with them will make it a breeze to follow along with the rest of the article.
Also, if you’re not familiar with Convolutions or Convolution Neural Networks (CNNs) in general, here is a great resource with good visualizations that explains how CNNs work.

Audio Samples

Introduction

Speech enhancement is crucial area of research in the field of signal processing, with applications in improving the quality, clarity and intelligibility of speech signals in various environments. It involves processes to reduce background noise, remove unwanted acoustic artifacts, and amplify desired speech components. This technology finds applications in diverse fields such as telecommunications, hearing aids, speech recognition systems, audio/video conferencing, and broadcast media. [1] [2]
Traditional signal processing methods, such as spectral subtraction [3] and Wiener filtering [4], are required to produce an estimate of noise spectra and then the clean speech given the additive noise assumption. These methods work well with stationary noise process, but may not generalize well to nonstationary or structured noise types such as dogs barking, baby crying, or traffic horn. Recent advances in deep learning have led to significant improvements in speech enhancement performance. However, there is still much to explore in terms of model architectures and training approaches.
The model in question is based on a supervised approach described in the paper "Speech Denoising in the Waveform Domain with Self-Attention" by Kong et al. This method, called CleanUNet, operates directly on raw waveforms and leverages self-attention mechanisms to refine bottleneck representations in the U-Net network. [5]
The primary goal of the CleanUNet model is to effectively remove background noise from recorded speech while maintaining the perceptual quality and intelligibility of the speech signals. This model addresses the limitations of traditional signal processing methods by utilizing the increased computational power of deep neural networks to achieve state-of-the-art results in speech enhancement.
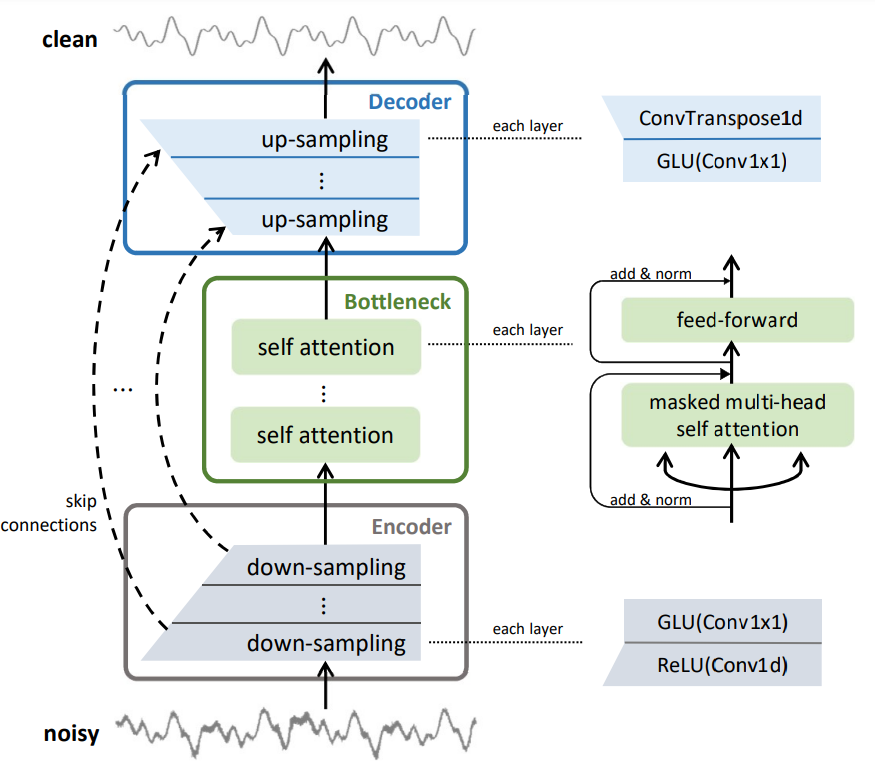
The architecture of CleanUNet consists of three main components: an encoder, a bottleneck with self-attention blocks, and a decoder. The encoder compresses the input waveform into a lowerdimensional representation -- an embedding, which is then refined by the self-attention blocks in the bottleneck. Finally, the decoder reconstructs the denoised waveform from the refined representation. The model uses causal convolutions to ensure low-latency processing, making CleanUNet suitable for real-time applications.

The following sections will cover the model's architecture, the training supervision strategies, and the loss functions used to optimize its performance.
Furthermore the model will be benchmarked on the VoiceBank + Demand dataset [6] using various objective metrics (e.g. PESQ [7]). This evaluation will include a comparison with other state-of-theart models to demonstrate how the model outperforms them on various benchmarks.

The Model's Architecture

Problem Setting

1. $\hat{\mathbf{x}} = f(\mathbf{x}_\text{noisy}) \approx \mathbf{x}$
2. $f$ is causal: the $t$-th element of the output $\hat{\mathbf{x}_t}$ is only a function of the previous observation $\mathbf{x}_\text{1:t}$

The U-Net Architecture

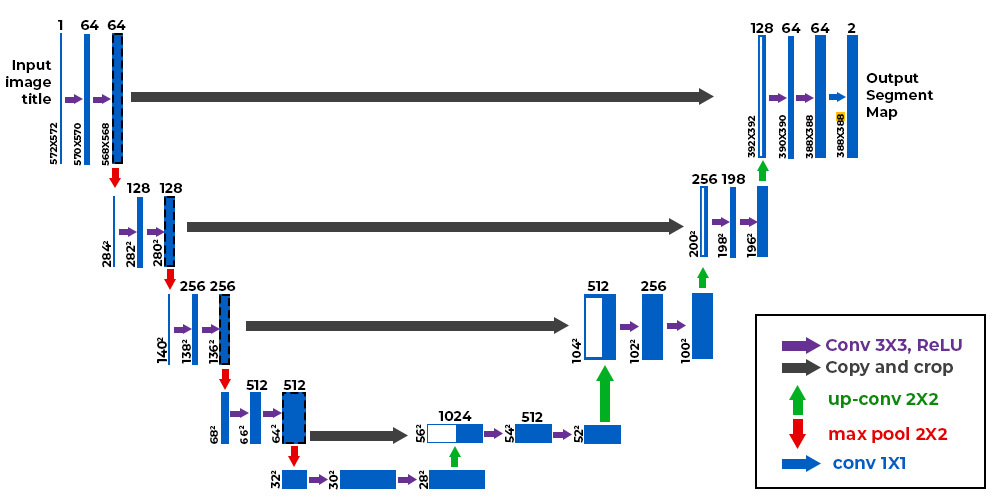
The Encoder and Decoder

• $W_1$ and $W_2$ are weight matrices.
• $b_1$ and $b_2$ are bias vectors.
• $\sigma$ is the sigmoid activation function.
• $\odot$ denotes element-wise multiplication.

The Bottleneck

The Loss Function

▶ STFT?? Click here to read more!

Sound can be represented in two primary forms: as a waveform in the time domain and as a frequency spectrum in the frequency domain. Each representation has its uses, and transforming between them helps analyze and process sound signals effectively.

Waveform

The waveform representation plots the sample values over time and illustrates the changes in the sound’s amplitude. This is also known as the time domain representation of sound. This type of visualization is useful for identifying specific features of the audio signal such as the timing of individual sound events, the overall loudness of the signal, and any irregularities or noise present in the audio.
Formally, a sound signal can be represented as a waveform $x(t)$ which is a function of time. In digital form, it is sampled at discrete time steps and becomes $x[n]$, where $n$ is the index of the sample.
$x(t)$ is converted into a discrete signal by sampling at intervals $T_s$ (sampling period), and the discrete representation is: $$ x[n] = x(nT_s) \quad \text{for } n \in \mathbb{Z} $$

This is an example of a trumpet sound. This visualization plots the amplitude of the signal on the yaxis and time along the x-axis. In other words, each point corresponds to a single sample value that was taken when this sound was sampled.

Frequency Spectrum

The frequency spectrum of a signal reveals which frequencies are present in the signal and their respective magnitudes (and phases, if phase information is included). For a time-domain signal $x[n]$, the frequency spectrum shows the amplitude of each frequency component in the signal. The spectrum is computed using the discrete Fourier transform or DFT. The DFT converts a discretetime signal from the time domain to the frequency domain. It computes a finite set of frequency components from a finite number of samples of the signal.
Mathematically, for a discrete-time signal $x[n]$ with $N$ samples, the DFT is defined as: $$ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j 2 \pi k n / N} \quad \text{for } k = 0, 1, \dots, N-1 $$ where $X[K]$ is the DFT coefficient for frequency bin $k$.
To recover the time-domain signal from the frequency-domain components, we apply the Inverse Discrete Fourier Transform (IDFT): $$ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{j 2 \pi k n / N} $$

This is a frequency spectrum plot for the same trumpet sound, it shows the strength of the various frequency components that are present in this audio segment. The frequency values are on the xaxis, usually plotted on a logarithmic scale, while their amplitudes are on the y-axis.

Short-Time Fourier Transform (STFT)

The Discrete Fourier Transform (DFT) provides the frequency components of the entire signal but doesn’t capture time-localized frequency changes, the spectrum only shows a frozen snapshot of the frequencies at a given instant.
To analyze how the frequency content evolves over time, we use the Short-Time Fourier Transform (STFT). The signal is divided into short overlapping frames or segments, typically lasting a few milliseconds. This is done to analyze the signal in shorter, manageable pieces because the frequency content of a signal can change over time. Then a window function (e.g., Hamming, Hanning) is applied to each segment to reduce edge effects and minimize discontinuities at the boundaries. For each windowed segment, we compute the Fourier Transform to obtain the frequency content. The Fourier Transform converts the time-domain signal into the frequency domain, giving a complex-valued output that represents both magnitude and phase. STFT segments the signal into shorter overlapping windows and applies the DFT to each segment. This produces a two-dimensional time-frequency representation. Given a signal $x[n]$, we multiply it by a window function $w[n]$ typically a Hann or Hamming window, which selects a portion of the signal. The STFT is computed as: $$ STFT(x, m, k) = \sum_{n=0}^{N-1} x[n] \cdot w[n - m] \cdot e^{-j 2 \pi k n / N} $$ where $m$ is the time index, and $k$ is the frequency index, and $w[n]$ is the window function.
The resulting spectra are then stacked together on the time axis to create the spectrogram. Each vertical slice in this image corresponds to a single frequency spectrum, seen from the top.
The STFT provides a Spectrogram which is a visual representation of the magnitude of the STFT coefficients $ \vert STFT(x, m, k) \vert $ , showing how the signal’s frequency content changes over time.
The window function controls how much of the signal is analyzed at a time. The window length affects the resolution: A longer window gives better frequency resolution but worse time resolution, whereas a shorter window gives better time resolution but worse frequency resolution.
In practice, we compute the FFT or the Fast Fourier Transform instead of the STFT for time complexity reasons. The FFT has the same steps as the STFT, but instead of computing the Fourier Transform for each window, we apply an efficient algorithm to compute the Discrete Fourier Transform (DFT). The most common algorithm used is the Cooley–Tukey algorithm [11].
The FFT algorithm reduces the computational complexity of calculating the DFT from $O(N^2)$ (Where $N$ is the number of samples) to $O(N\log(N))$. This makes it feasible to compute the STFT for large datasets and long signals efficiently.

In this plot, the x-axis represents time as in the waveform visualization but now the y-axis represents frequency in Hz. The intensity of the color gives the amplitude or power of the frequency component at each point in time, measured in decibels (dB).

Training Setup

The model

Data Preparation

Optimizer

1. Compute the gradients $g_t$ at time step $t$: $g_t = \nabla_\theta J(\theta_t) $, where $\theta_t$ are the model's parameters at time step $t$ and $\nabla_\theta J(\theta_t)$ is the gradient of the loss function $J(\theta_t)$ with respect to the parameters.
2. Update biased first moment estimate $m_t$ : $m_t = \beta_t m_\text{t-1} + (1-\beta_t)g_t$
3. Update biased second moment estimate $v_t$ : $v_t = \beta_t v_\text{t-1} + (1-\beta_2) g_t^2$
4. Compute bias-corrected first moment estimate $\hat{m_t}$ : $\hat{m_t} = \frac{m_t}{1-\beta_1^t}$
5. Compute bias-corrected second moment estimate $\hat{v_t}$ : $\hat{v_t} = \frac{v_t}{1-\beta_2^t}$
6. Update the parameters: $\theta_\text{t+1} = \theta_t - \alpha \frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon}$ where $\alpha$ is the learning rate and $\epsilon$ is a small constant to prevent division by zero

Evaluation and Benchmarking

• Perceptual Evaluation of Speech Quality (PESQ) [7]: It compares the enhanced speech signal with a reference clean signal and provides a score ranging from -0.5 to 4.5, with higher values indicating better quality. PESQ uses a model of human auditory perception to predict how a listener would perceive the quality of the speech signal, taking into account various distortions and degradations.
• Short-Time Objective Intelligibility (STOI) [15]: STOI measures the intelligibility of speech, which is how easily a listener can understand the speech signal. It provides a score between 0 and 1, with higher values indicating better intelligibility. STOI is based on a correlation coefficient between temporal envelopes of clean and degraded speech signals in short time frames. It focuses on the intelligibility aspect rather than the overall quality.
• Distortion of speech signal (CSIG): CSIG evaluates the perceived quality of the speech signal with a focus on the signal distortion. It ranges from 1 to 5, with higher scores indicating less distortion. CSIG assesses how much the speech signal has been distorted during the enhancement process, providing an indication of the signal fidelity.
• SNR (Signal-to-Noise Ratio): SNR is a measure of the ratio between the desired signal and the background noise. It is expressed in decibels (dB), with higher values indicating a cleaner signal. SNR quantifies the level of the speech signal relative to the noise, providing an indication of how well the model reduces noise in the enhanced speech.
• Background noise (CBAK): CBAK evaluates the quality of the background noise suppression. It ranges from 1 to 5, with higher scores indicating better noise suppression. CBAK focuses on how well the model suppresses the background noise while preserving the speech signal.
• Overall Quality (COVL): COVRL provides an overall quality score of the enhanced speech, considering both the speech signal and the background noise. It ranges from 1 to 5, with higher scores indicating better overall quality. COVRL gives a holistic evaluation of the enhanced speech, taking into account both the intelligibility and the naturalness of the speech as well as the background noise suppression
• Speech-to-Reverberation Modulation Energy Ratio (SRMR): SRMR measures the amount of reverberation in the speech signal. It provides a score where higher values indicate less reverberation and better speech quality. SRMR focuses on the temporal modulation characteristics of the speech signal and evaluates the amount of reverberation, which can affect the clarity and intelligibility of the speech.

References